Random Number Generator of an accumulative type
In this article I am going to tell about the operating principles and characteristic properties of Random Number Generator (RNG) used in the DiskCryptor.
RNG - this is a critically important security element of a disk encryption system, as it generates the keys with which data is encrypted. And it is exactly the RNG that is often a weak spot or a backdoor in a different sorts of proprietary and government certified encryption systems, because precision of an encryption algorithm\'s implementation and the data storage methods can be easily examined even without having an access to the source code, but RNG, however, is much more difficult to analyze.
It is possible to create a one-way strong RNG that will allow for a person, knowing a certain secret, to recover all the keys that were generated by it and to consequently compromise encrypted data. A good example of such case - the Dual_EC_DRBG standard, which has backdoor and is used in Windows, since Vista SP1.
The creation purposes and the objectives performed
The DiskCryptor\'s RNG purpose is to perform the following two objectives: generation of encryption keys and generation of a large volume of random data for disk wiping algorithms. For the first objective it is necessary to provide as big strength reserve as possible, and below are the key generation requirements that RNG has to meet:
- Issue of numbers, statistically indistinguishable from random ones.
- Impossibility of an algorithmic prediction of the sequences being generated or the ones generated earlier even with the availability of a large amount of random numbers made in the past.
- The requirement No.2 has to retain its maximum possible integrity state even when an attacker knows an internal state of the generator.
- It is imperative to provide a maximum possible strength reserve that exceeds attacker\'s capabilities by manifold.
- Simple and clear, even for a non-professional, architecture and operating principles.
For the second objective, when generating a large volume of random numbers, requirements for RNG differ:
- Issue of numbers, statistically indistinguishable from random ones.
- Impossibility to predict sequences being generated without knowing an internal state of the generator.
- Maximum possible performance.
RNG for key generation
RNG for key generation that is used in the DiskCryptor, belongs to the accumulative RNG type with multiple sources of entropy. RNG of this type accumulates minor entropy values over a long period of time, following that it is capable of issuing a truly random sequence having size of up to 640 bytes, afterwards, pseudo-random sequences will follow up until a new accumulation of entropy.
As a basis for the RNG architecture, SHA-512 hash function and AES-256block cipher are taken. The choice of this function is made because of its simplicity, good performance and high reliability, though less stringent requirements are set for hash in this case than, for example, when using it for the digital signatures. The hash function used, has to have the following properties:
- Statistically random output on casually-random input data.
- Dependence of each output bit of hash on all the input bits. On a change of one bit on an entry, no less than a half of output bits has to alter.
- One-sidedness. Recovery of an entry data based on its hash value has to be impossible. This characteristic is very desirable, but a part of RNG properties are retained even without its presence.
Simplified block scheme of RNG looks the following way:
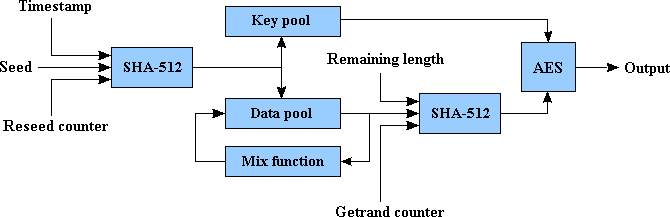
Accumulation of random numbers
This is being done by hashing a seed together with a timestamp and a reseed counter. Adding both timestamp and reseed counter prevents generation of identical hash values on a same seed. The obtained hash is added to the random number pool by means of addition with respect to base 28 with existing content of the pool, and that creates a dependence of content of the pool on all random number additions made earlier.
The pool has the size of 640 bytes, which allows for the accumulation of the maximum of 5120 bits of entropy. On one addition of a seed, the size of entropy increases by the maximum of 512 bits, therefore the SHA-512 hash size requires no less then 10 reseeds, for fully filling up the pool. In addition to having the big pool for data accumulation, RNG also has the second one, the keys pool. This pool has the size of 256 bits and it is never being outputted, even indirectly, but is used as a key for the AES-256, with which output data is encrypted.
Mixing up the pool
Mixing up the pool - this is the operation that is performed with the objective to make all the bits in the pool to become dependent on each other. The goal of mixing - is to create the reliance of each bit being generated, on all the content of the pool, but at the same time not to decrease the maximum entropy, as would have happened on hashing the whole pool at the moment of issuing random numbers. The mixing operation has a characteristic of being one-sided, meaning that, knowing a state of the pool after a mixing, it is impossible to restore its previous state. This characteristic is directly based on the corresponding properties of the SHA-512 hash.
Mixing is being done with the help of mix function (the rnd_pool_mix function in the source code). During the mixing process, the pool is being divided into 10 parts, each having the size of 64 bytes, and to each part, a value of SHA-512 hash of all the pool content is being added. This process can be presented as follows:
pool0 = pool0 + SHA(pool0 || pool1 ... pooln)
pool1 = pool1 + SHA(pool0 + SHA(pool0 || pool1 ... pooln) || pool1 ... pooln)
...
Mixing is performed in either of the following three cases: before generation of a random byte sequence, after it, and in the case when entire content of the pool has been expended in the process of generation, and issuing of data has gone to a second round. The first mixing is required for the creation of dependency of output data on all the pool content. The second mixing protects the generated keys from an attacker who has an opportunity to read the contents of memory after generation (for example with the Cold Boot attack). The third mixing allows for the use of new entropy that is being added to the pool in the process of random number generation, and it also creates an additional remoteness between the already generated and the subsequent random numbers.
Random numbers retrieval
The random numbers retrieval function receives generator\'s output data from its internal state. Retrieval of random numbers is done by taking the SHA-512 hash from a part of the pool, random generated blocks counter (getrand counter), and a size of a remaining part of a requested data (remaining length), and encryption of an obtained hash with AES-256 key, received from the keys pool. Getrand counter and remaining length are needed to eliminate the possibility of generation of two identical output blocks on a same content of the pool. A situation having the same content in the pool is an unlikely one, due to its mixing, nevertheless, I believe that an additional safety measure would only be of a benefit. The generation process can be presented as follows:
rand0 = SHA(pool0 || counter || length)
rand1 = SHA(pool1 || counter + 1 || length - 64)
...
randn = SHA(pooln || counter + n || length - 64*n)
In the process of retrieval of every 512 bits of data, twice, a gathering of additional entropy takes place. After reaching the maximum possible n (having the 640 bytes pool size, it equals 10), pool mixing takes place, and the subsequently issued data will not be truly random, but partially pseudorandom. The strength of this construction to withstand a risk of being compromised, having minor values of an effective entropy (that is, pseudorandom numbers), is based on the total strength of SHA-512 and AES-256, that gives a strength reserve even in a case of fully breaking of one of these cryptoprimitives. The source code for number retrieval from the pool, you can find in the function rnd_get_bytes.
Sources of entropy
Sources of entropy, - is the RNG element, the importance of which is hard to overvalue. It is precisely these sources that are responsible for an effective entropy, which is accumulated by RNG, and consequently, an effective entropy of generated keys. Howsoever good the entropy retrieval algorithm might be, but a poor source of entropy can place the RNG security in jeopardy. And vice versa, - a good source of randomness, in some cases, may "stretch" the security of a weak retrieval algorithm. Sources of entropy should be approached to with a much greater paranoia, than the RNG algorithm, as the strength of these sources is practically non-provable and can vary by many magnitudes on different assumptions about an attacker\'s resources and potential. So therefore, it is prudent to follow the rule of "You can\'t spoil a good thing. Plenty is no plague." And thus, it is best to use as many different sources of randomness, as possible. Adding another additional source, will not lower the strength, but only might to increase it, in certain cases. Consequently, what is needed here, is - redundancy, more redundancy, and even more redundancy.
Having redundancy, - is a very good thing, but one should not rely on an empirical value of its size, as it just may happen, that an attacker may be able to read the majority of entropy sources used, and the remaining inaccessible sources he may be capable to pick up or predict. Therefore, there is the need to have at least a simplest numerical basis for an effective size of entropy in relation to an attacker, who has various capabilities. For the start, we should define what kind of leverage a hypothetical attacker may have.
- The simplest version, - is when an attacker has absolutely no access to a computer in a moment of random number generation, he also does not know the exact moment of generation, nor has an information about the state of a system on that moment either. This model corresponds to the most likely kind of an attacker, and this model has the maximum possible safety of all the sources of entropy. Later on, one of the versions of strength calculation will be given with regard to this model.
- A more complicated version, - is when an attacker has a partial access to a computer and knows an approximate (within the milliseconds range) time of random number generation, and when he also has the access to a part of system information on that moment. Practically, this model corresponds to a potential that an attacker may have in a multi-user environment, when he has no administrative privileges in there. Later on, strength calculation for this model will also be presented, and exactly these kind of numbers should be taken as a basis for giving an assessment for having a minimum acceptable strength.
- And finally the third version, - when an attacker has a full access to a system. It is obvious, that it is impossible to be protected in such a case, as an attacker can take control of and to replace any sources of entropy, and also can have a direct influence upon internal state of the RNG, or to replace the RNG completely with his own one. This version corresponds to a kind of an attacker, which has administrative privileges on a system that he is attacking, and there is no, nor there can be a defense from him. Therefore, under no circumstances you must generate keys or work with a confidential data on a system that can be controlled by someone other than you. Otherwise, your security is literally hairbreadth to none.
The sources of entropy that are used in the DiskCryptor\'s RNG are separated into two types: fast sources, working in the kernel-mode, and slow sources, working in the user-mode. The first ones a residing together with the RNG inside the driver, and the second ones reside in the dcapi.dll, and the data from them is periodically transmitted to the driver. First, let us examine a set of functions of the kernel, used as a kernel-mode sources of randomness. Their main property is inaccessibility of their direct reading by an attacker that has a limited access to a system, but a portion of their bits may be predictable, and so in the table that is presented below there are two values for each source: minimum and maximum. The values are true on a condition that the use of these sources is no frequent than 10 times per second, on a more numerous use an effective entropy of each call decreases.
| Function | Dependency | Minimum entropy | Maximum entropy |
|---|---|---|---|
| PsGetCurrentProcess | On the process invoking reseed | 0 | 2 |
| PsGetCurrentProcessId | On the process invoking reseed | 0 | 2 |
| KeGetCurrentThread | On the thread invoking reseed | 1 | 4 |
| PsGetCurrentThreadId | On the thread invoking reseed | 0 | 2 |
| KeGetCurrentProcessorNumber | On the number of current processor | 0 | 2 |
| KeQueryInterruptTime | On all interrupts in the system | 8 | 16 |
| KeQueryPriorityThread | On the thread priority | 0 | 1 |
| KeQueryPerformanceCounter | RTC (Real Time Clock) | 4 | 8 |
| __rdtsc | CPU timestamp counter | 16 | 24 |
| ExGetPreviousMode | Previous mode of the thread execution | 0 | 1 |
| IoGetInitialStack | Initial stack of the thread | 0 | 1 |
| IoGetTopLevelIrp | Last IRP (Input/output Request Packet) in the queue | 0 | 2 |
| MmQuerySystemSize | Size of the system memory | 0 | ? |
| ExUuidCreate | PRNG of the Windows kernel | 8 (?) | ? |
| RtlRandom | Predictable value, but may be altered by other drivers | 0 | ? |
| KeQueryTickCount | Number of ticks of the counter from the moment of system\'s boot | 2 | 4 |
| IoGetStackLimits | Stack limits for the current thread | 0 | ? |
| Total: | 39 | 75 |
Thus, we can see that on an average we get 39-75 random bits on one reseed operation. This is not enough if reseed is carried out once, therefore DiskCryptor retrieves entropy from fast functions in the moment of a first thousand disk I/O operations after the system\'s start. Even if we are to assume that the time of I/O operations execution is practically constant, then on the minimum we would have no less than 1 bit of entropy per reseed (because predicting the time of reading data from a disk with the nanosecond precision looks like a fiction), that in total would amount to no less than 1000 bits of effective entropy right after the system\'s boot. Subsequently, the fast source of entropy is being used less, and namely in the moment of some not very frequent system events, and in the moment of random number generation.
Besides using fast kernel-mode entropy sources, RNG also uses slow user-mode sources. Several API functions and also user actions (mouse movement, pressing of keys) are used as user-mode sources. At the start of the program, Windows\'s RNG CryptoAPI CryptGenRandom function is used once, as the source of entropy. Recent studies show that this RNG is weak and in a protracted period of time it issues pseudorandom numbers, as it rarely replenishes entropy, and thus using it more than once is not justified. It is difficult for me to name the value of its effective entropy, but apparently it has to be no less than 32 bits, otherwise RNG would have had a very short period, which can be discovered with a simplest of tests. Mouse movements are used as the source of entropy the whole time the program is working. This is a very good source of entropy even on its own accord, as the time between the two mouse communications is wide in comparison with CPU clocks, and even from this time alone it is possible to confidently gather 16 random bits at a time. Extra 2-3 random bits can be taken off from mouse cursor coordinates and presses of mouse keys. Keyboard keys presses in the program\'s window are also used by RNG, and both the time of press and release, as well as the key\'s code are sent to it. This guarantees, that even in the absence of other sources of randomness, the effective entropy of the keys being generated, cannot be less than the entropy of your password, as the password is also used in key generation. It is also important, that these sources of entropy are inaccessible for reading by a local attacker with limited privileges, since if attacker\'s privileges are high enough to intercept keyboard presses, then encryption loses all its meaning.
In addition to one-time and persistent sources of entropy described above, the program also uses recurrent entropy sources, information from which is collected every 5 seconds as long as the program works. The list of functions used, and approximate value of amount of random bits receive from them, is presented in the table below.
| Function | Minimum entropy | Maximum entropy | Inaccessible to local attacker |
|---|---|---|---|
| GetDesktopWindow | 0 | 1 | 0 |
| GetForegroundWindow | 2 | 4 | 2 |
| GetShellWindow | 0 | 1 | 0 |
| GetCapture | 0 | ? | ? |
| GetClipboardOwner | 0 | ? | ? |
| GetOpenClipboardWindow | 0 | ? | ? |
| GetCurrentProcessId | 0 | 1 | 0 |
| GetCurrentThreadId | 0 | 1 | 0 |
| GetFocus | 0 | 1 | ? |
| GetActiveWindow | 0 | ? | ? |
| GetKBCodePage | 0 | ? | ? |
| GetCursor | 0 | 2 | ? |
| GetLastActivePopup | 0 | ? | ? |
| GetProcessHeap | 0 | 2 | 0 |
| GetQueueStatus | 0 | 2 | 0 |
| GetInputState | 0 | ? | ? |
| GetMessageTime | 0 | ? | ? |
| GetOEMCP | 0 | ? | ? |
| GetCursorInfo | 8 | 16 | 8 |
| GetCaretPos | 0 | ? | ? |
| GetThreadTimes | 4 | 8 | 0 |
| GetProcessTimes | 4 | 8 | 0 |
| GetProcessMemoryInfo | 4 | 8 | 0 |
| QueryPerformanceCounter | 8 | 16 | 8 |
| GlobalMemoryStatusEx | 4 | 8 | 0 |
| EnumWindows | 128 | 256 | 128 |
| Total: | 162 | 335 | 146 |
In total we have 146 bits, that are guaranteed to be inaccessible even to a local attacker. That is not too much, but nevertheless, already lies beyond the capabilities of attackers having modern day technology.
Fast PRNG for generation of large volume of random numbers
The aforementioned RNG is designed to generate small amount of random numbers with a large strength reserve. This scheme\'s efficiency, however, is quite low and therefore it is unsuited for generation of gigabytes of random numbers that are needed for the algorithms to securely wipe disk sectors on encryption. For this purpose DiskCryptor has the pseudorandom number generator that is built with the utmost simplicity, but nonetheless its durability is based on the strength of the AES.
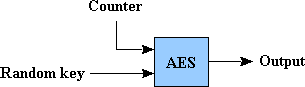
Here in this scheme, the main RNG is used as the source of entropy, and with its help a random AES key is generated on the first initialization of the generator. Output of pseudorandom numbers is done by the process of encryption, using this key, of sequentially incrementing 128 bit counter. Statistical characteristics of output data are fully ensured by the AES algorithm. On the completion of generator\'s work, the key is destroyed, and it becomes impossible to distinguish an obtained data from a random data. This scheme has the property of being simple and sufficiently safe for its purpose.
List of publications used
- Peter Gutmann, "Software Generation of Practically Strong Random Numbers", 1998
- Elaine Barker, John Kelsey "NIST Special Publication 800-90", National Institute of Standards and Technology, March 2007
- John Kelsey, Bruce Schneier, David Wagner, Chris Hall, "Cryptanalytic Attacks on Pseudorandom Number Generators", Springer-Verlag London, UK, 1998